基本原理

本节主要介绍 DSLab 平台储能规划的基本原理。

功能定义

DSLab 提供的储能规划功能。

功能说明

优化目标

配网侧储能规划的优化目标为经济性最优，主要考虑了储能设备的投资成本和运行成本，其中运行成本包括储能运行的可变运维成本、从上级电网的购电成本（若有）等。优化目标可以表示为以下公式：

$$\min \left( \sum_{t=1}^{T} P_t \cdot G_{\text{mw}}[t] + \sum_{e=1}^{E} \sum_{tp=1}^{TP} E_{\text{ss}\text{typ}[e,tp]} \cdot \text{esscost}[tp] \right)$$

式中：

• $G_{\text{mw}}[t]$ 为时刻 $t$ 外购电功率；
• $P_t$ 为 $t$ 时刻外购电价格；
• $\text{esscost}[tp]$ 为储能接入成本（包含投资成本和运行成本）。

约束条件和决策变量

优化模型中所考虑的约束条件和决策变量如下表所示，其中决策变量主要包括储能的接入位置、配置容量以及 8760h 的运行策略。与此同时，如果系统中存在柔性负荷，算法还会对柔性负荷曲线进行调节，以配合实现最经济的新能源消纳。

模型分类	参数类型	参数名称	参数说明
固定负荷	约束条件	8760h 曲线	储能规划时将始终保证负荷得到满足
柔性负荷	约束条件	负荷可削减上限	负荷每日电量的最大可削减量
		负荷可调节时段	每日24h 允许进行负荷转移或者削减的时段
	决策变量	柔性负荷的实际运行曲线	柔性负荷的实际运行曲线
分布式电源	约束条件	8760h 曲线	储能规划时电源的实际出力曲线
上级电网	约束条件	基准电压	平衡节点的基准电压
		最大反送电功率	向上级电网反送电的最大功率，可设置成0，即代表100%的新能源消纳
储能设备	约束条件	SOC上下限	SOC上下限
		单日最大循环充放电次数	循环充放电次数是指储能充放电累计的电量除以储能充放电深度
		最大充放电功率	最大充放电功率
		储能日内始末SOC一致	储能日内始末SOC一致
	决策变量	储能的配置容量	储能的配置容量
		储能的8760h充放电策略	储能的8760h充放电策略
全局参数	约束条件	节点电压的上下限	节点电压的上下限
		全网可接入的储能最大容量	全网可接入的储能最大容量
	决策变量	储能可接入的待选节点位置	包括所有 10kv 馈线上的母线节点，或者由用户指定的可接入母线节点
物理模型	约束条件	交流潮流约束	交流潮流约束

算法流程

优化模型求解：

上述优化模型如果直接求解，计算量非常大，计算效率也不可接受。针对这一问题，本算法将上述优化模型拆分为两个层次进行求解：上层优化模型用于规划储能的设备容量、并网位置；下层优化模型用于优化系统潮流分布、降低网损，保证节点电压水平。两层次的优化模型求解思路如下图所示：

两层次优化求解模型

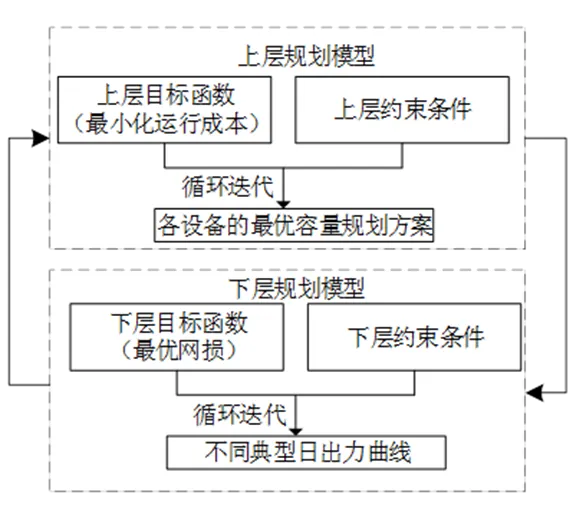
上层优化模型：

上层采用混合整数规划算法进行优化模型求解。混合整数规划通常采用分支定界法（branch-and-bound，B&B），隐式枚举所有可能的组合方案，从理论上能够求得问题的最优解。随着运筹学理论的发展，割平面法（cutting planes）应运而生，其核心思想是在寻优过程中动态添加割平面约束，裁剪可行域中不包含整数可行解的区域，让凸包（convex hull）尽可能暴露在可行域的边界，加速寻优过程。分支定界法与割平面法的结合，形成了分支-割平面法（branch-and-cut，B&C），极大地提升了混合整数规划（MIP）的求解效率。

下层优化模型：

下层采用非线性内点法进行求解。内点法最初是作为一种线性规划算法提出的，旨在解决单纯形法计算量随变量规模急剧增加的问题。内点法从初始可行集合的内点出发，利用牛顿法沿着可行方向，求出使目标函数值下降的后继内点，再沿另一个可行方向求出使目标函数值继续下降的内点，重复以上步骤，从可行域内部向最优解迭代，得出一个由内点组成的序列，使得目标函数值严格单调下降。

内点法存在很多变种类型，其中对数障碍函数法（Barrier Method）的效果比较理想。它的迭代次数相对稳定，与系统规模大小弱相关。其主要步骤如下图所示：