构网型储能变流器-平均模型-v1

案例介绍

构网型储能变流器-平均模型由平均化电气拓扑、功率同步环节、电压外环、电流内环和调制环节等模块构成，还附加了标幺化、倍乘等值、量测与输出、多短路比测试实现，直流侧为储能电池，后续可拓展斩波控制、穿越控制、脱网控制等模块，模型整体架构如下图所示。

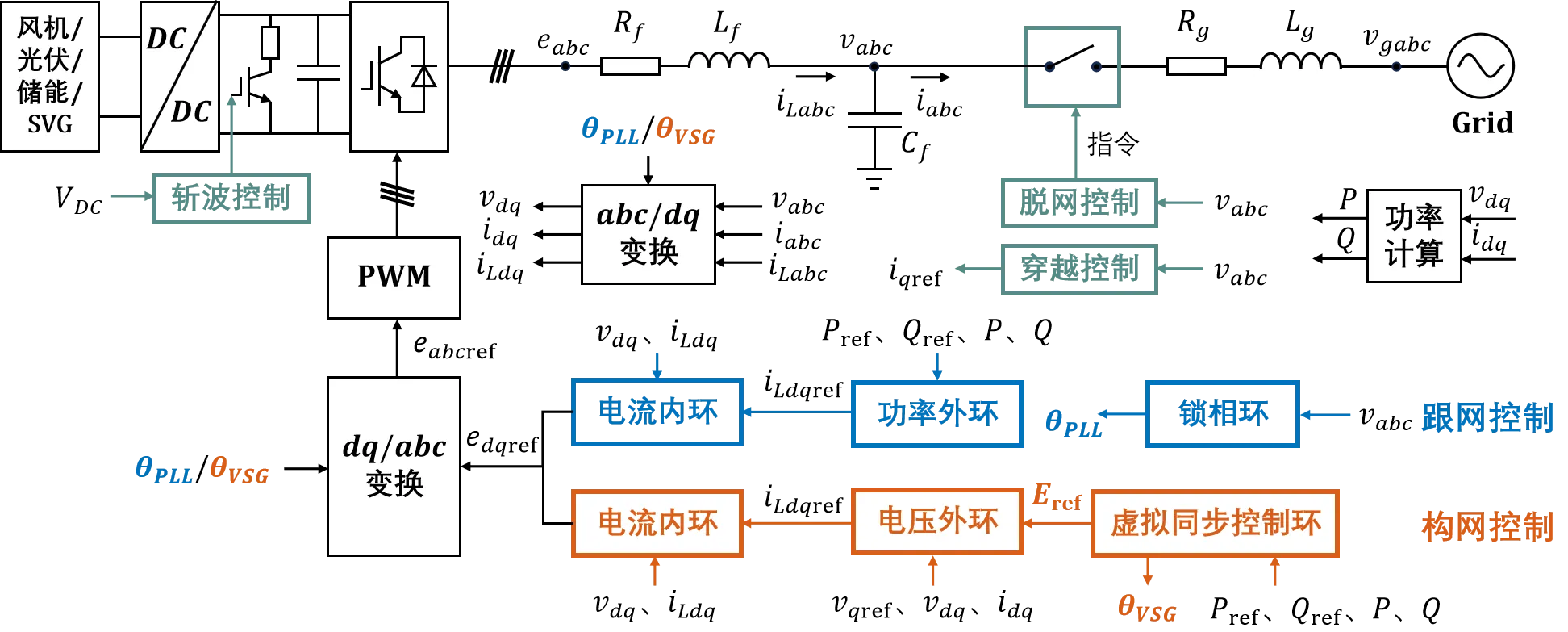跟网/构网型变流器并网系统整体架构示意图

模型已封装为元件，具备单元测试回路，可单独使用，也可在其他算例中调用。

元件图形

使用方法说明

适用场景

构网型储能变流器-平均模型支持单机或接入大规模电力系统算例的仿真测试，适用于以下分析场景：

• 小信号稳定性分析
• 不同短路比下的变流器并网适应性测试
• 考虑系统功角、频率、电压的电网稳定性分析
• 高比例新能源接入下的系统支撑能力评估
• 跟网型与构网型控制策略的对比研究

适用范围

• 建议步长范围：1–50 μs  
• 当前参数设置下建议短路比范围：2~7

功能概述

• 变流器并网系统的发电单元除储能外，还可以接入风机、光伏或SVG，以满足不同的研究需求
• 构网型变流器控制的构网控制方式支持虚拟同步控制与下垂控制的切换

 

算例介绍

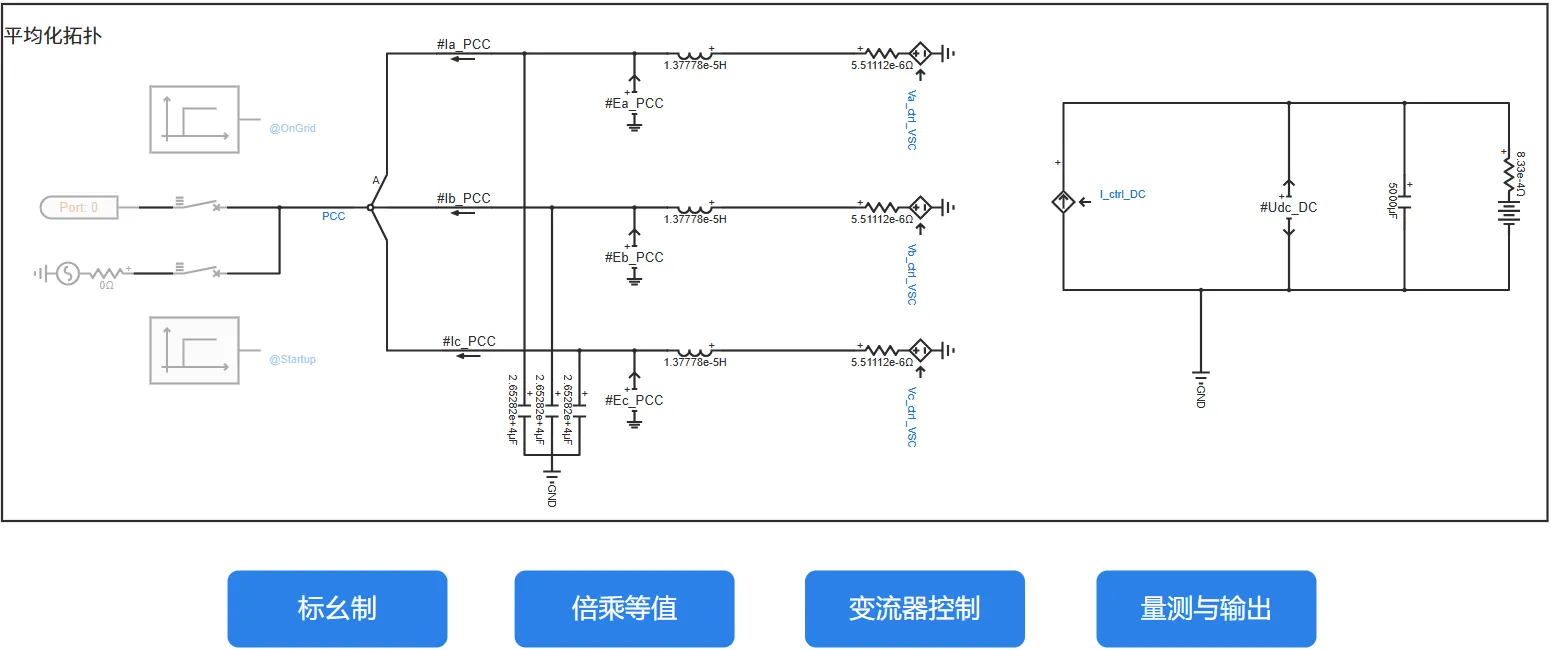
构网型储能变流器-平均模型由电气主拓扑、标幺制、倍乘等值、变流器控制、量测与输出等五个模块组成。

电气主拓扑由蓄电池、直流电容、受控电流源组成的直流侧和受控电压源、交流滤波器、电压源组成的交流侧，以及功率设定和单元测试构成，实现平均化变流器等效建模。

• 功率设定输出由用户设定的输出有功、无功功率参考值，并包含输出小信号扰动功率的功能

• 单元测试中设置经线路阻抗与理想电压源相连，连接阻抗的大小由用户设置，系统的短路比在量测与输出模块中计算并输出。

  

  电气主拓扑

  

  功率设定与单元测试

标幺制处理使仿真中除时间外的电气量均为标幺值，便于参数的通用化设置。为使得所构建的变流器模型适用于各种电压等级及功率送出场景，需要构造一个物理概念清晰、使用方便的变流器模型标幺制系统，将控制环节中的量测值、参考值、元件参数、控制参数等均转换为标幺值，经过调试和优化可以得到一套通用的控制参数，实现变流器模型标幺化。

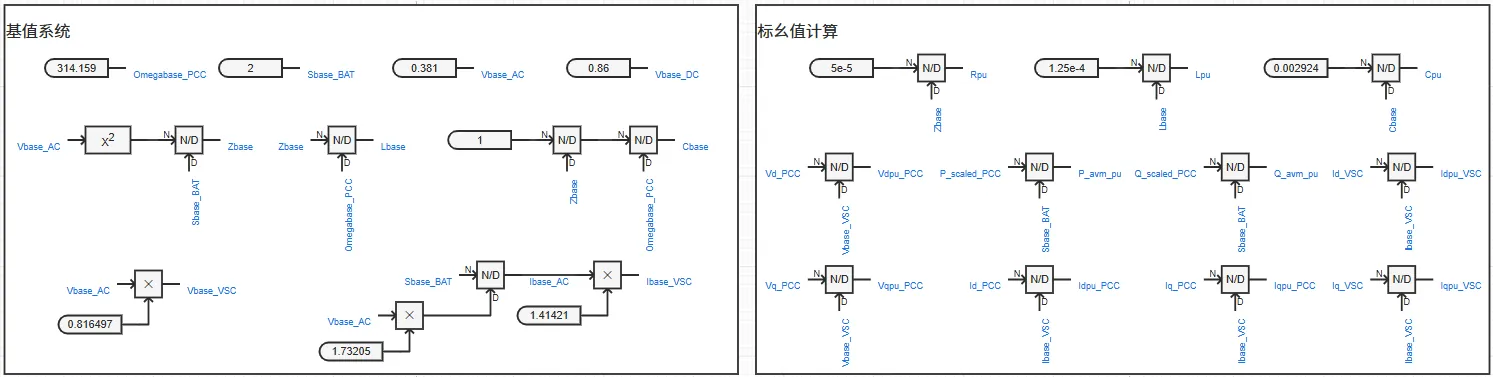标幺制系统

倍乘等值的基本原理为：按设备额定电压、额定容量、并联数量变化倍数线性缩放电阻、电感、电容等参数，并保持电压、电流标幺值不变（有名值需要折算），可在简化模型规模的同时，使等效模型在并网点呈现与真实多机系统相似的功率输出和动态响应，从而满足系统级稳定性分析的需求。

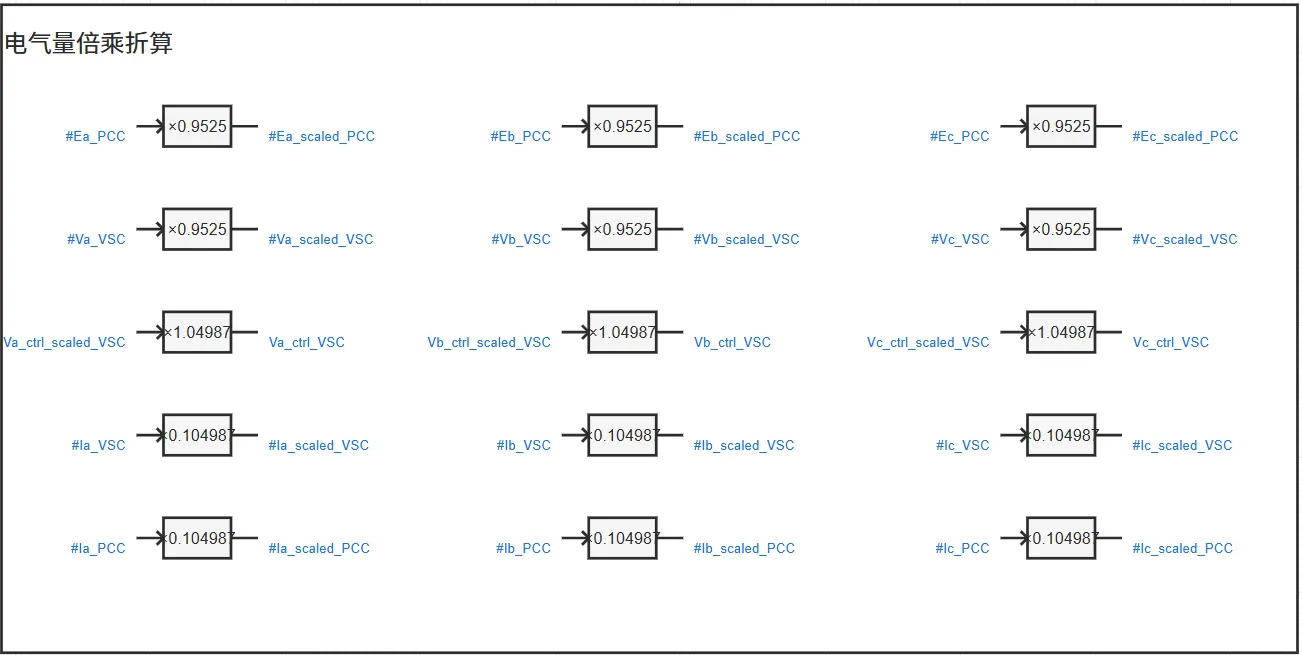倍乘等值

变流器控制由坐标变换、功率计算、功率同步环节、电压外环控制、电流内环控制、调制模块和平均化控制等部分组成，实现输出功率的控制。其中功率同步环节包含有功-频率控制和无功-电压控制两个部分，控制策略可选择虚拟同步控制或下垂控制，两种控制策略的切换可在参数组中进行设置。此外，平均化变流器的控制信号通过功率平衡法计算得到。

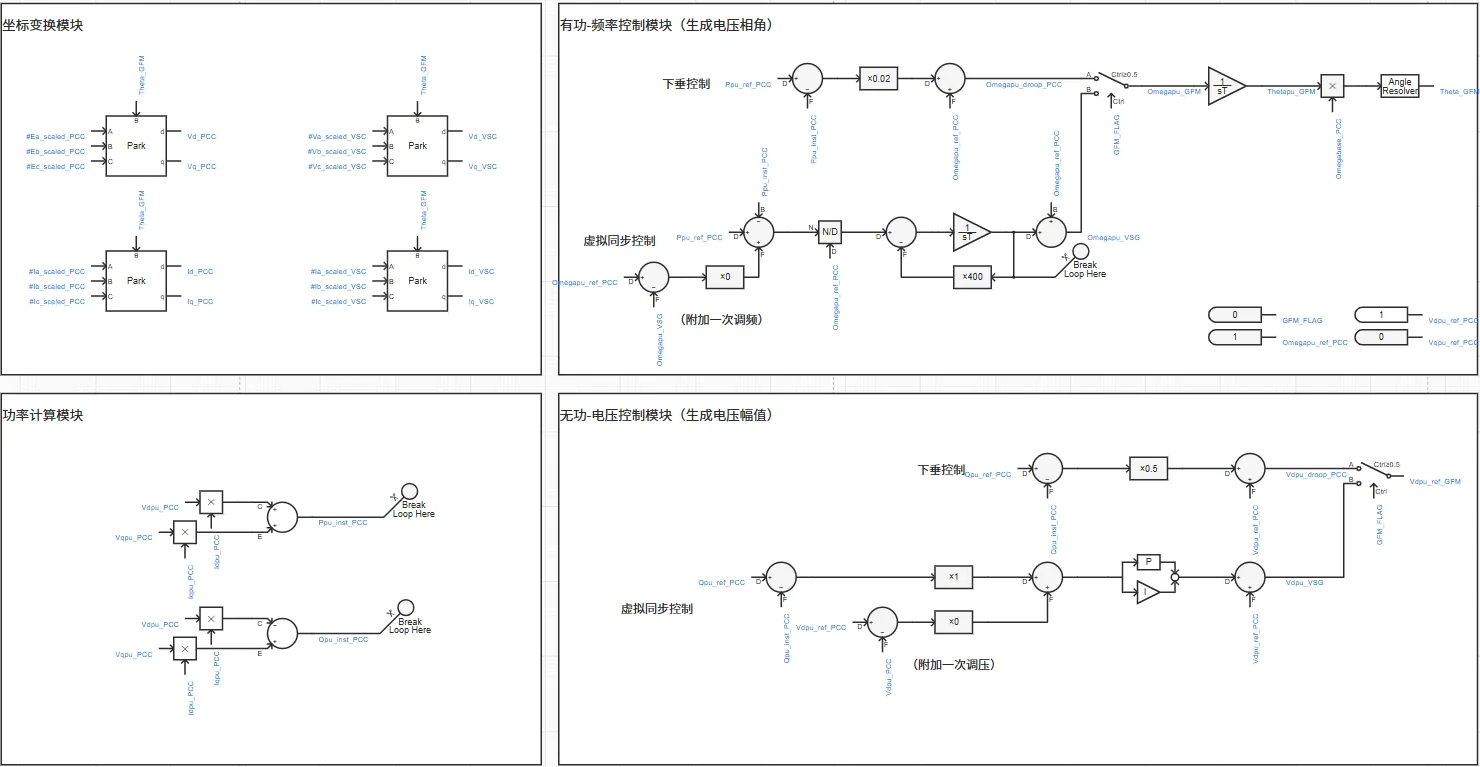变流器控制

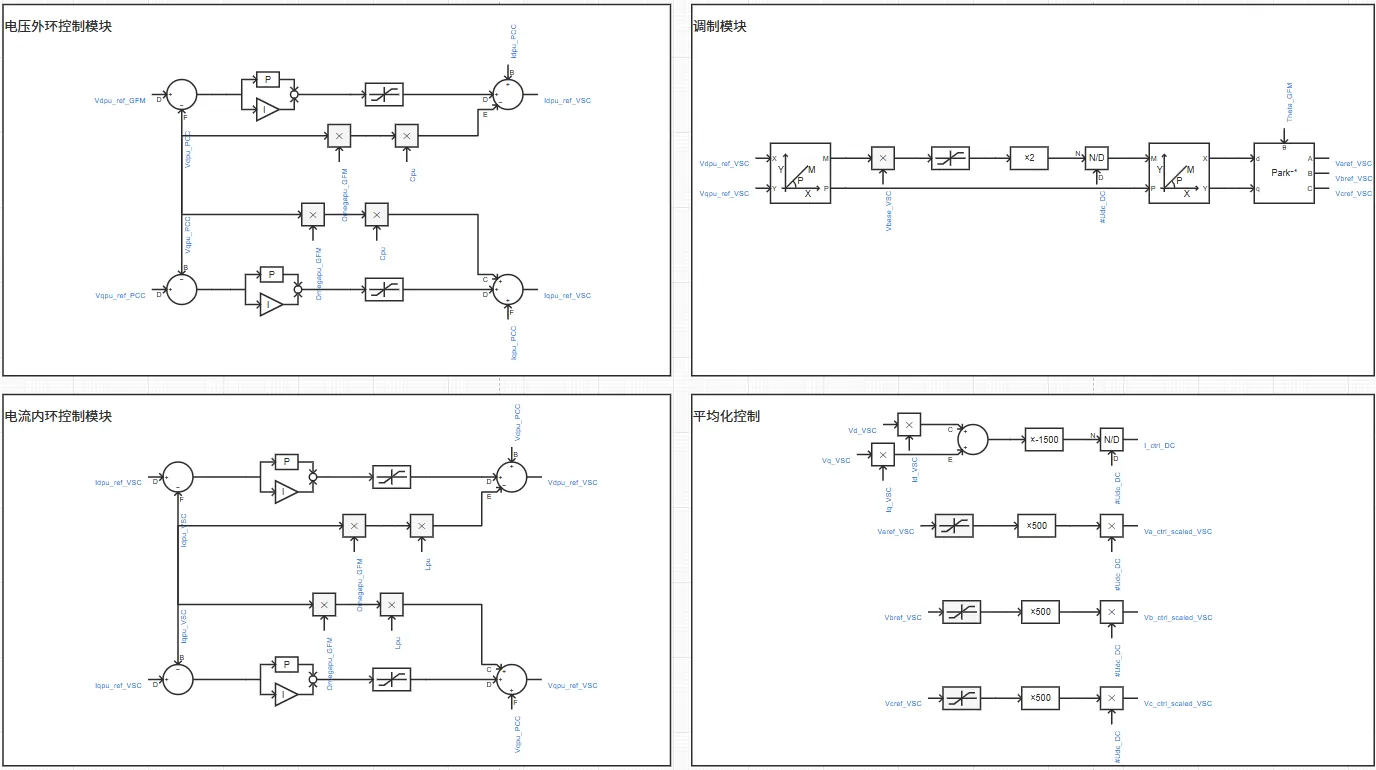变流器控制

量测与输出模块量测控制环节所需电气量，计算并输出用户关注的电气量。

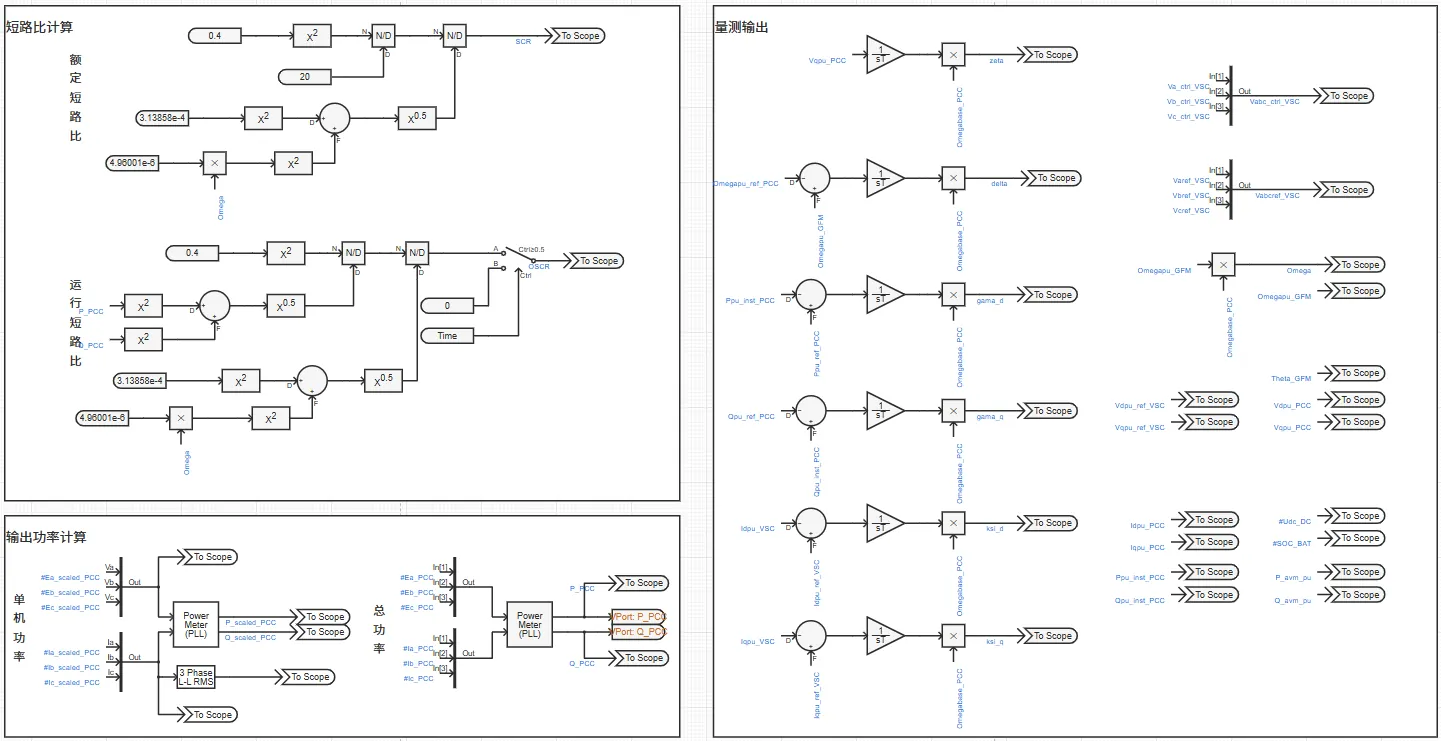量测与输出

算例仿真测试

针对构网型储能变流器-平均模型分别进行了小信号状态空间模型验证和并网适应性测试。

小信号状态空间模型验证

依据构网型储能变流器-平均模型构建了全阶小信号状态空间模型，如下式所示。

$$\Delta \dot x = A\Delta x + B\Delta u$$

其中：

$$x = {[\delta ,\omega ,E,{\gamma _d},{\gamma _q},\;{\xi _d},{\xi _q},{i_d},{i_q},{i_{Ld}},{i_{Lq}},{v_d},{v_q}]^{\rm{T}}}$$ $$u = {\left[ {{P_{{\rm{ref}}}},{Q_{{\rm{ref}}}},{v_{d{\rm{ref}}}},{v_{q{\rm{ref}}}}} \right]^{\rm{T}}}$$ $$\tiny{A} = \begin{bmatrix} 0&1&0&0&0&0&0&0&0&0&0&0&0\\[4mm] 0&{ - \dfrac{{{D_p} + {K_w}/{\omega _0}}}{J}}&0&0&0&0&0&{ - \dfrac{{{v_{d0}}}}{{J{\omega _0}}}}&{ - \dfrac{{{v_{q0}}}}{{J{\omega _0}}}}&0&0&{ - \dfrac{{{i_{d0}}}}{{J{\omega _0}}}}&{ - \dfrac{{{i_{q0}}}}{{J{\omega _0}}}}\\[4mm] 0&0&0&0&0&0&0&{ - {K_q}{v_{q0}}}&{{K_q}{v_{d0}}}&0&0&{{K_q}{i_{q0}} - {K_u}}&{ - {K_q}{i_{d0}}}\\[4mm] 0&0&{\dfrac{1}{{{T_Q}}}}&0&0&0&0&{ - {K_Q}{K_q}{v_{q0}}}&{{K_Q}{K_q}{v_{d0}}}&0&0&{ - {K_Q}({K_u} - {K_q}{i_{q0}}) - 1}&{ - {K_Q}{K_q}{i_{d0}}}\\[4mm] 0&0&0&0&0&0&0&0&0&0&0&0&{ - 1}\\[4mm] 0&{ - {C_f}{v_{q0}}}&{\dfrac{{{K_{o{\rm{2}}}}}}{{{T_Q}}}}&{\dfrac{1}{{{T_{o{\rm{2}}}}}}}&0&0&0&{1 - {K_Q}{K_{o{\rm{2}}}}{K_q}{v_{q0}}}&{{K_Q}{K_{o{\rm{2}}}}{K_q}{v_{d0}}}&{ - 1}&0&{ - {K_{o{\rm{2}}}}({K_Q}({K_u} - {K_q}{i_{q0}}) + 1)}&{ - {C_f}{\omega _0} - {K_Q}{K_{o{\rm{2}}}}{K_q}{i_{d0}}}\\[4mm] 0&{{C_f}{v_{d0}}}&0&0&{\dfrac{1}{{{T_{o{\rm{2}}}}}}}&0&0&0&1&0&{ - 1}&{{C_f}{\omega _0}}&{ - {K_{o{\rm{2}}}}}\\[4mm] {\dfrac{{{v_{g0}}\sin {\delta _0}}}{{{L_g}}}}&{{i_{q0}}}&0&0&0&0&0&{ - \dfrac{{{R_g}}}{{{L_g}}}}&{{\omega _0}}&0&0&{\dfrac{1}{{{L_g}}}}&0\\[4mm] {\dfrac{{{v_{g0}}\cos {\delta _0}}}{{{L_g}}}}&{ - {i_{d0}}}&0&0&0&0&0&{ - {\omega _0}}&{ - \dfrac{{{R_g}}}{{{L_g}}}}&0&0&0&{\dfrac{1}{{{L_g}}}}\\[4mm] 0&{ - \dfrac{{{C_f}{K_{i{\rm{2}}}}{v_{q0}}}}{{{L_f}}}}&{\dfrac{{{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}}}{{{L_f}{T_Q}}}}&{\dfrac{{{K_{i{\rm{2}}}}}}{{{L_f}{T_{o{\rm{2}}}}}}}&0&{\dfrac{1}{{{L_f}{T_{i{\rm{2}}}}}}}&0&{ - \dfrac{{{K_{i{\rm{2}}}}({K_Q}{K_{o{\rm{2}}}}{K_q}{v_{q0}} - 1)}}{{{L_f}}}}&{\dfrac{{{K_Q}{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}{K_q}{v_{d0}}}}{{{L_f}}}}&{ - \dfrac{{{K_{i{\rm{2}}}} + {R_f}}}{{{L_f}}}}&0&{ - \dfrac{{{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}({K_Q}({K_u} - {K_q}{i_{q0}}) + 1)}}{{{L_f}}}}&{ - \dfrac{{{K_{i{\rm{2}}}}({C_f}{\omega _0} + {K_Q}{K_{o{\rm{2}}}}{K_q}{i_{d0}})}}{{{L_f}}}}\\[4mm] 0&{\dfrac{{{C_f}{K_{i{\rm{2}}}}{v_{d0}}}}{{{L_f}}}}&0&0&{\dfrac{{{K_{i{\rm{2}}}}}}{{{L_f}{T_{o{\rm{2}}}}}}}&0&{\dfrac{1}{{{L_f}{T_{i{\rm{2}}}}}}}&0&{\dfrac{{{K_{i{\rm{2}}}}}}{{{L_f}}}}&0&{ - \dfrac{{{K_{i{\rm{2}}}} + {R_f}}}{{{L_f}}}}&{\dfrac{{{C_f}{K_{i{\rm{2}}}}{\omega _0}}}{{{L_f}}}}&{ - \dfrac{{{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}}}{{{L_f}}}}\\[4mm] 0&{{v_{q0}}}&0&0&0&0&0&{ - \dfrac{1}{{{C_f}}}}&0&{\dfrac{1}{{{C_f}}}}&0&0&{{\omega _0}}\\[4mm] 0&{ - {v_{d0}}}&0&0&0&0&0&0&{ - \dfrac{1}{{{C_f}}}}&0&{\dfrac{1}{{{C_f}}}}&{ - {\omega _0}}&0 \end{bmatrix}$$ $${B} = {\begin{bmatrix} 0&{\dfrac{1}{{J{\omega _0}}}}&0&0&0&0&0&0&0&0&0&0&0\\[4mm] 0&0&{{K_q}}&{{K_Q}{K_q}}&0&{{K_Q}{K_{o{\rm{2}}}}{K_q}}&0&0&0&{\dfrac{{{K_Q}{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}{K_q}}}{{{L_f}}}}&0&0&0\\[4mm] 0&0&{{K_u}}&{{K_Q}{K_u} + 1}&0&{{K_{o{\rm{2}}}}({K_Q}{K_u} + 1)}&0&0&0&{\dfrac{{{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}({K_Q}{K_u} + 1)}}{{{L_f}}}}&0&0&0\\[4mm] 0&0&0&0&1&0&{{K_{o{\rm{2}}}}}&0&0&0&{\dfrac{{{K_{i{\rm{2}}}}{K_{o{\rm{2}}}}}}{{{L_f}}}}&0&0 \end{bmatrix} ^{\rm{T}}}$$

参数列表如下：

符号	物理意义	取值
J	虚拟转动惯量	100p.u.
KD	虚拟阻尼系数	400p.u.
Kq	无功权重系数	1.00p.u.
KQ	无功-电压比例系数	0.10p.u.
TQ	无功-电压积分时间常数	0.10s
Ko	电压外环比例系数	2.00p.u.
To	电压外环积分时间常数	0.40s
Ki	电流内环比例系数	2.00p.u.
Ti	电流内环积分时间常数	0.40s
Vdref	并网电压 d 轴参考值	1.00p.u.
Vqref	并网电压 q 轴参考值	0p.u.
Kω	调频系数	0p.u.
Ku	调压系数	0p.u.
Rf0	原始滤波电阻	2.00mΩ
Lf0	原始滤波电感	5.00mH
Cf0	原始滤波电容	73.10μF
V0	原始额定电压	0.381kV
SB0	原始单机额定容量	0.05MVA
N	并联数量	10
VB	额定电压	0.40kV
SB1	单机额定容量	2.00MVA
Pref	有功功率参考值	0.90p.u.
Qref	无功功率参考值	0.10p.u.
SCR	系统短路比	5.0
X/R	系统电抗电阻比	5.0

由小信号状态空间模型计算得到并网系统特征根分布如下图所示，验证了系统的稳定性。

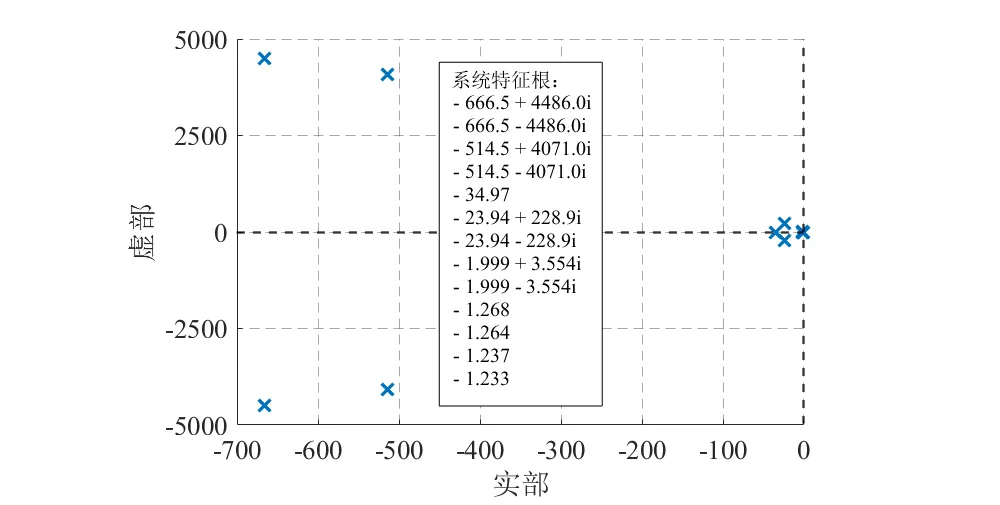特征根分布

小扰动下构网型储能变流器-平均模型状态空间方程理论计算结果与电磁暂态仿真结果基本相同，各电气量均方根误差均小于$5×10^{-4}$，验证了模型的准确性。

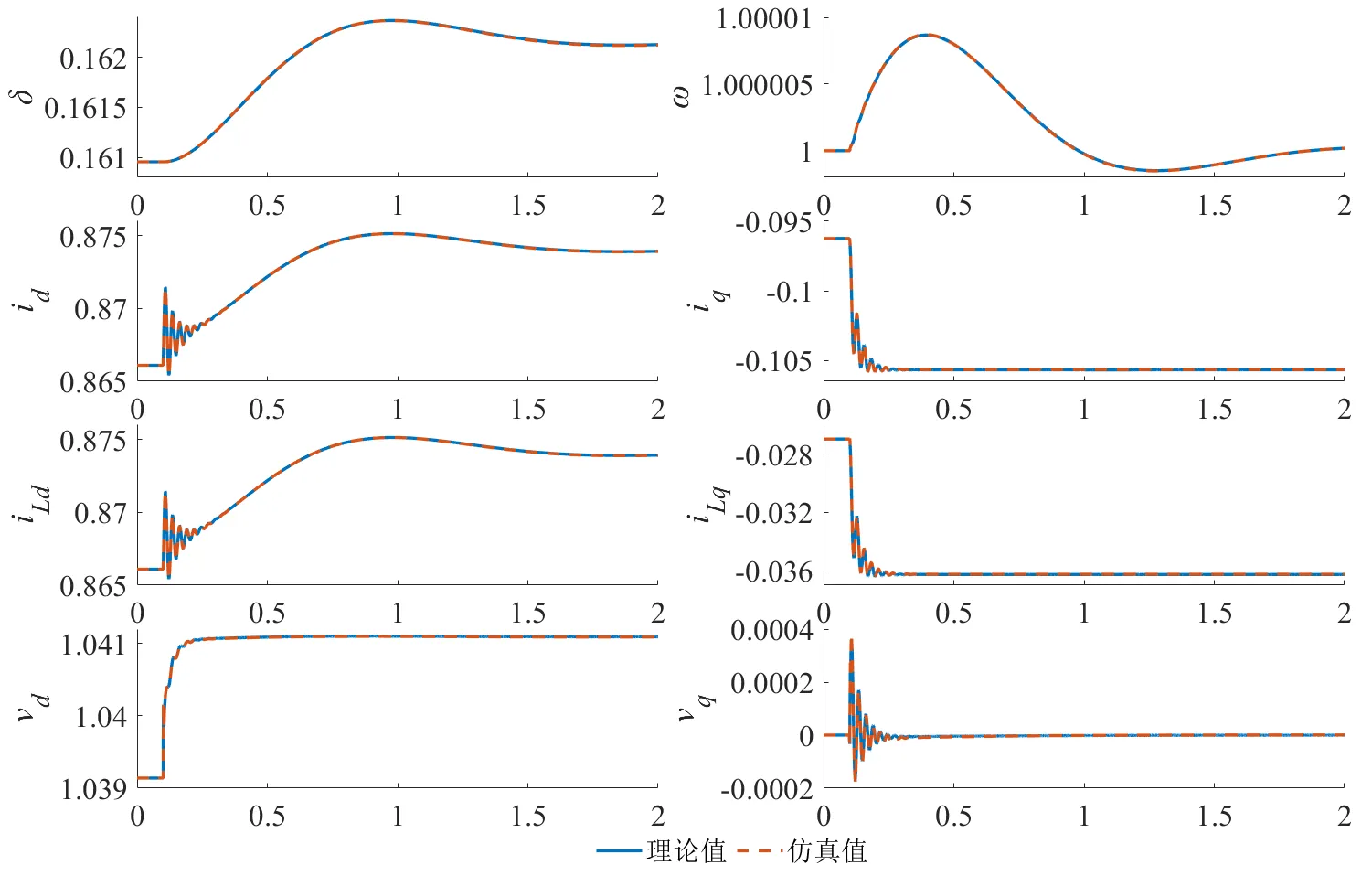小扰动验证

并网适应性测试

对构网型储能变流器-平均模型进行了多短路比下的并网适应性测试。由下图可知，当系统短路比为2~7时，系统稳定性随短路比和电抗电阻比变化较小，系统均保持稳定，而当短路比小于2或大于7时，系统稳定性随着电抗电阻比增大而减弱，甚至失稳。

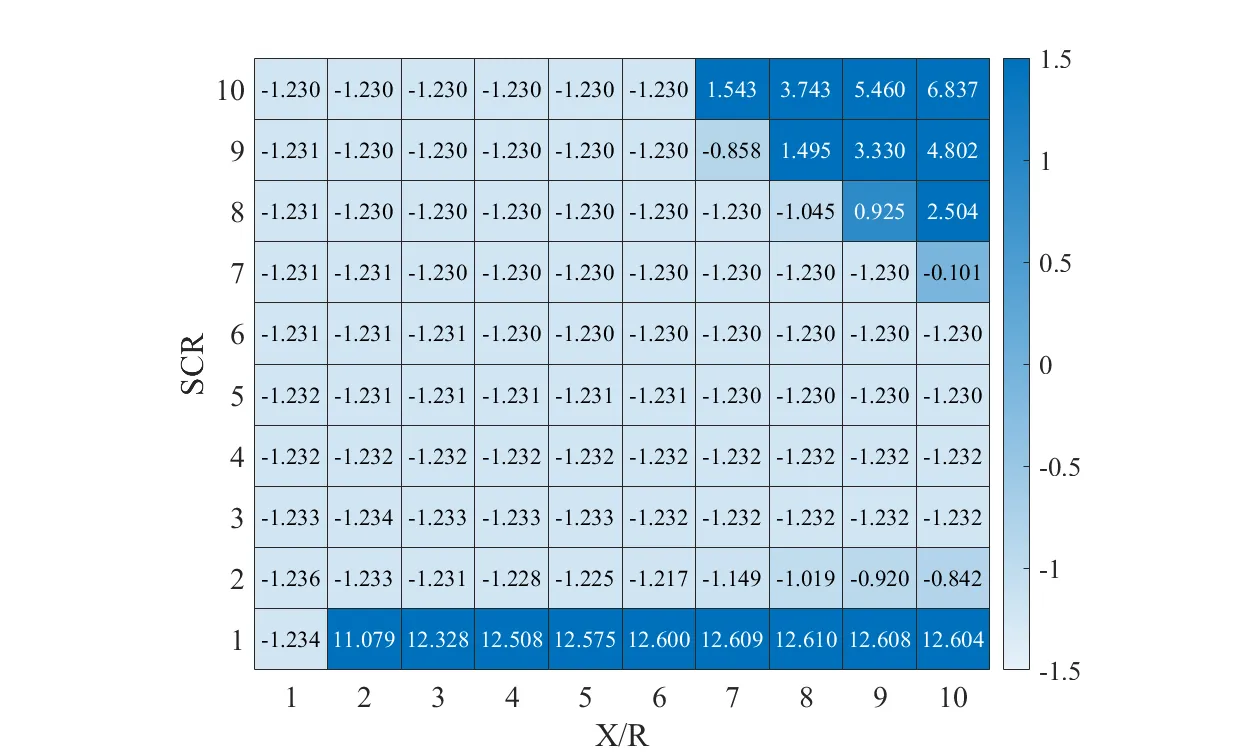构网型变流器并网系统主导特征根实部热力图

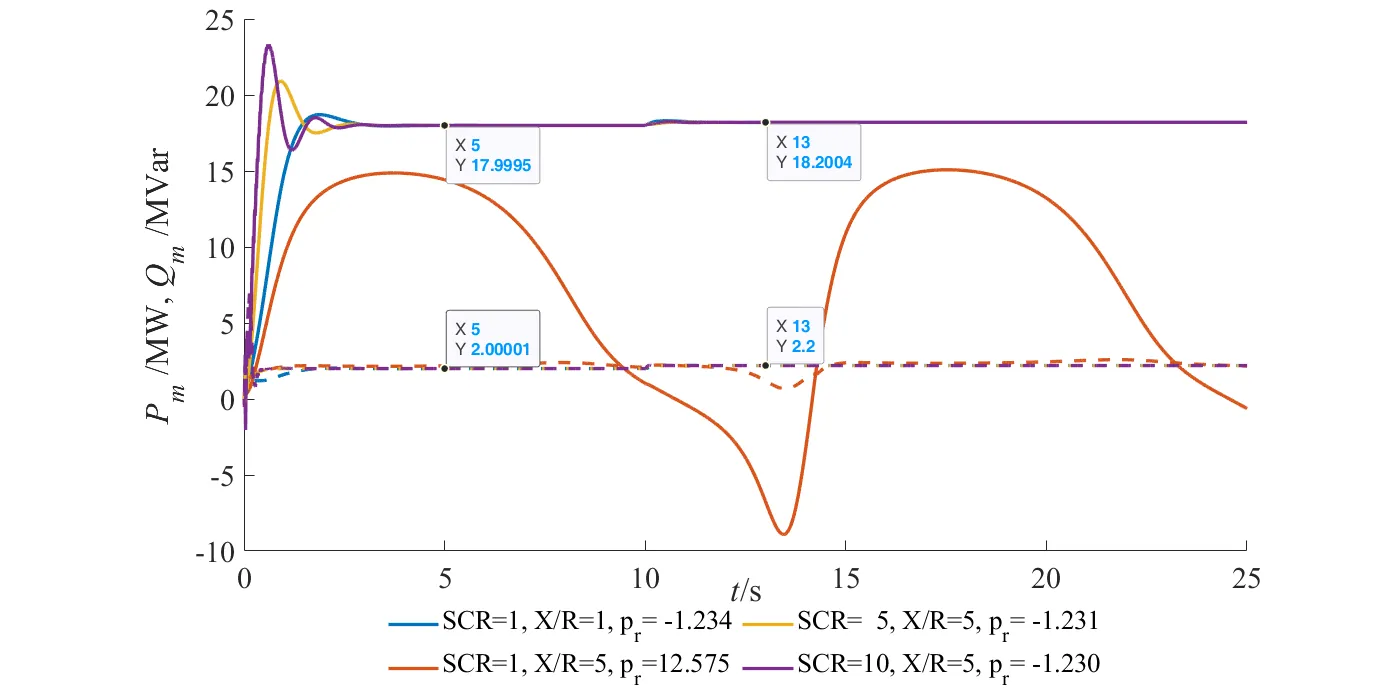机端功率

模型地址

点击打开模型地址：构网型储能变流器-平均模型

附录

参数

基本设置

基本设置

参数名	键名	类型 [单位]	描述
并联数量	num	实数	并联储能设备数量
并网点电压	Vpcc	实数 [kV]	交流端口线电压有效值
电压初始相位	Init_Phase	实数 [Deg]	电压初始相位
单机额定容量	Sbase	实数 [MVA]	单机额定容量（1~3MVA）
有功功率参考值	Ppu_ref_PCC	实数 [p.u.]	有功功率参考值
无功功率参考值	Qpu_ref_PCC	实数 [p.u.]	无功功率参考值

构网控制参数设置

构网控制参数设置

参数名	键名	类型 [单位]	描述
构网控制方式	GFM_FLAG	选择	下垂/虚拟同步控制选择
有功-频率下垂系数	Dp_VSC	实数 [p.u.]	有功-频率下垂系数
无功-电压下垂系数	Dq_VSC	实数 [p.u.]	无功-电压下垂系数
虚拟转动惯量	J_VSC	实数 [kg·m^2]	虚拟同步机转子惯量系数
阻尼系数	KD_VSC	实数 [kg·m^2/s]	阻尼系数
无功-电压比例系数	KQ_VSC	实数 [p.u.]	无功-电压比例系数
无功-电压积分时间常数	TQ_VSC	实数 [p.u.]	无功-电压积分时间常数
无功权重系数	Kq_VSC	实数 [p.u.]	无功权重系数
一次调频系数	Kf_VSC	实数 [p.u.]	附加一次调频控制系数（取零则为无调频附加控制）
一次调压系数	Ku_VSC	实数 [p.u.]	附加一次调压控制系数（取零则为无调压附加控制）
电压外环比例系数	Ko_VSC	实数 [p.u.]	VSC 控制中，电压外环 PI 环节的比例系数
电压外环积分时间常数	To_VSC	实数 [s]	VSC 控制中，电压外环 PI 环节的积分时间常数
电压外环限幅	Olim_VSC	实数 [p.u.]	VSC 控制中，电压外环 PI 环节的限幅
电流内环比例系数	Ki_VSC	实数 [p.u.]	VSC 控制中，电流内环 PI 环节的比例系数
电流内环积分时间常数	Ti_VSC	实数 [s]	VSC 控制中，电流内环 PI 环节的积分时间常数
电流内环限幅	Ilim_VSC	实数 [p.u.]	VSC 控制中，电流内环 PI 环节的限幅

潮流设置

潮流设置

参数名	键名	类型 [单位]	描述
Bus Type	BusType	选择	节点类型
Injected Active Power	pf_P	实数 [MW]	节点注入有功功率
Injected Reactive Power	pf_Q	实数 [MVar]	节点注入无功功率
Bus Voltage Magnitude	pf_V	实数 [p.u.]	母线电压幅值
Bus Voltage Angle	pf_Theta	实数 [Deg]	母线电压相位
Lower Voltage Limit	pf_Vmin	实数 [p.u.]	母线电压下限
Upper Voltage Limit	pf_Vmax	实数 [p.u.]	母线电压上限
Lower Reactive Power Limit	pf_Qmin	实数 [MVar]	无功功率下限
Upper Reactive Power Limit	pf_Qmax	实数 [MVar]	无功功率上限

事件设置

事件设置

参数名	键名	类型 [单位]	描述
并网时间	OnTime	实数 [s]	储能并网运行时刻
启动时间	Startup_Time	实数 [s]	启动时间
功率设定改变时间	ChargeSwitch	实数 [s]	小扰动时间

量测设置

量测设置

参数名	键名	类型 [单位]	描述
有功量测(MW)	P_PCC	虚拟引脚（输出）	有功量测(MW)
无功量测(MVar)	Q_PCC	虚拟引脚（输出）	无功量测(MVar)

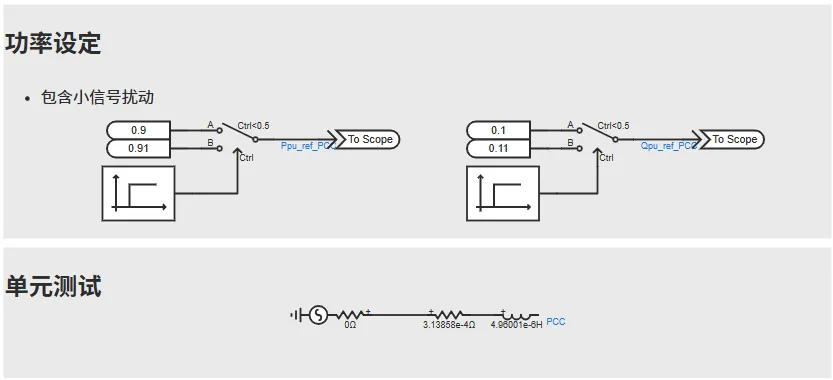
单元测试

单元测试

参数名	键名	类型 [单位]	描述
UnitTest	UnitTest	布尔	单元测试开关，打开时接入外部测试电路。
线路电阻	R	实数 [Ω]	线路等效电阻
线路电感	L	实数 [H]	线路等效电感

引脚

引脚名	键名	类型	维度	描述
AC	0	电气	3 × 1	AC