跳到主要内容

Park 变换器

元件定义​

该元件实现 Park 变换和逆 Park 变换计算。

元件说明​

属性​

CloudPSS 元件包含统一的属性选项，其配置方法详见 参数卡 页面。

参数​

Configuration​

Configuration

参数名键名类型 [单位]描述
NameName文本元件名称
此处输入Park变换器的名称（可缺省）
Direction of TransformationDirection选择变换方向
选择变换的方向为Park变换或逆Park变换
Rotating Frame AlignmentAlignment选择旋转轴对齐
选择坐标变换的d轴与A相对齐或滞后90度

引脚​

引脚名键名类型维度描述
Theta0输入1 x 1相角输入端口
d1输入1 x 1逆Park变换时d轴的输入端口
q2输入1 x 1逆Park变换时q轴的输入端口
A3输出1 x 1逆Park变换时a相的输出端口
B4输出1 x 1逆Park变换时b相的输出端口
C5输出1 x 1逆Park变换时c相的输出端口
A6输入1 x 1Park变换时a相的输入端口
B7输入1 x 1Park变换时b相的输入端口
C8输入1 x 1Park变换时c相的输入端口
d9输出1 x 1Park变换时d轴的输出端口
q10输出1 x 1Park变换时q轴的输出端口

使用说明​

坐标位置
坐标位置

当选择 d 轴与 a 相对齐时，Park 变换及逆 Park 变换的计算公式为：

  • Park 变换

[UdUqU0]=23[cos⁡θcos⁡(θ−2π/3)cos⁡(θ+2π/3)−sin⁡(θ)−sin⁡(θ−2π/3)−sin⁡(θ+2π/3)1/21/21/2][UaUbUc]\begin{gathered}\begin{bmatrix}U_\mathrm{d}\\U_\mathrm{q}\\U_0\end{bmatrix}=\frac23\begin{bmatrix}\cos\theta&\cos(\theta-2\pi/3)&\cos(\theta+2\pi/3)\\-\sin(\theta)&-\sin(\theta-2\pi/3)&-\sin(\theta+2\pi/3)\\1/2&1/2&1/2\end{bmatrix}\begin{bmatrix}U_\mathrm{a}\\U_\mathrm{b}\\U_\mathrm{c}\end{bmatrix}\end{gathered}

  • 逆 Park 变换

[UaUbUc]=[cos⁡θ−sin⁡(θ)1cos⁡(θ−2π/3)−sin⁡(θ−2π/3)1cos⁡(θ+2π/3)−sin⁡(θ+2π/3)1][UdUqU0]\begin{bmatrix}U_\mathrm{a}\\U_\mathrm{b}\\U_\mathrm{c}\end{bmatrix}=\begin{bmatrix}\cos\theta&-\sin(\theta)&1\\\cos(\theta-2\pi/3)&-\sin(\theta-2\pi/3)&1\\\cos(\theta+2\pi/3)&-\sin(\theta+2\pi/3)&1\end{bmatrix}\begin{bmatrix}U_\mathrm{d}\\U_\mathrm{q}\\U_0\end{bmatrix}

注意：传统 Park 变换中，d 轴超前 q 轴。dq 轴位置如上图红线所示。PSCAD 中采用了 q 轴超前 d 轴，如上图蓝线所示。因此相同输入下，本元件得出的 q 轴分量与 PSCAD 的结果正负相反。

坐标位置
坐标位置

当选择 d 轴滞后 a 相 90°时，dq 轴位置如上图绿线所示。Park 变换及逆 Park 变换的计算公式为：

  • Park 变换

[UdUqU0]=23[sin⁡(θ)sin(θ−2π/3)sin⁡(θ+2π/3)cos⁡θcos⁡(θ−2π/3)cos⁡(θ+2π/3)1/21/21/2][UaUbUc]\begin{gathered}\begin{bmatrix}U_\mathrm{d}\\U_\mathrm{q}\\U_0\end{bmatrix}=\frac23\begin{bmatrix}\sin(\theta)&sin(\theta-2\pi/3)&\sin(\theta+2\pi/3)\\\cos\theta&\cos(\theta-2\pi/3)&\cos(\theta+2\pi/3)\\1/2&1/2&1/2\end{bmatrix}\begin{bmatrix}U_\mathrm{a}\\U_\mathrm{b}\\U_\mathrm{c}\end{bmatrix}\end{gathered}

  • 逆 Park 变换

[UaUbUc]=[sin⁡(θ)cos⁡θ1sin⁡(θ−2π/3)cos⁡(θ−2π/3)1sin⁡(θ+2π/3)cos⁡(θ+2π/3)1][UdUqU0]\begin{gathered}\begin{bmatrix}U_\mathrm{a}\\U_\mathrm{b}\\U_\mathrm{c}\end{bmatrix}=\begin{bmatrix}\sin(\theta)&\cos\theta&1\\\sin(\theta-2\pi/3)&\cos(\theta-2\pi/3)&1\\\sin(\theta+2\pi/3)&\cos(\theta+2\pi/3)&1\end{bmatrix}\begin{bmatrix}U_\mathrm{d}\\U_\mathrm{q}\\U_0\end{bmatrix}\end{gathered}

下图展示了四种常用的Park变换类型的区别以及和各商用仿真软件的对应关系。

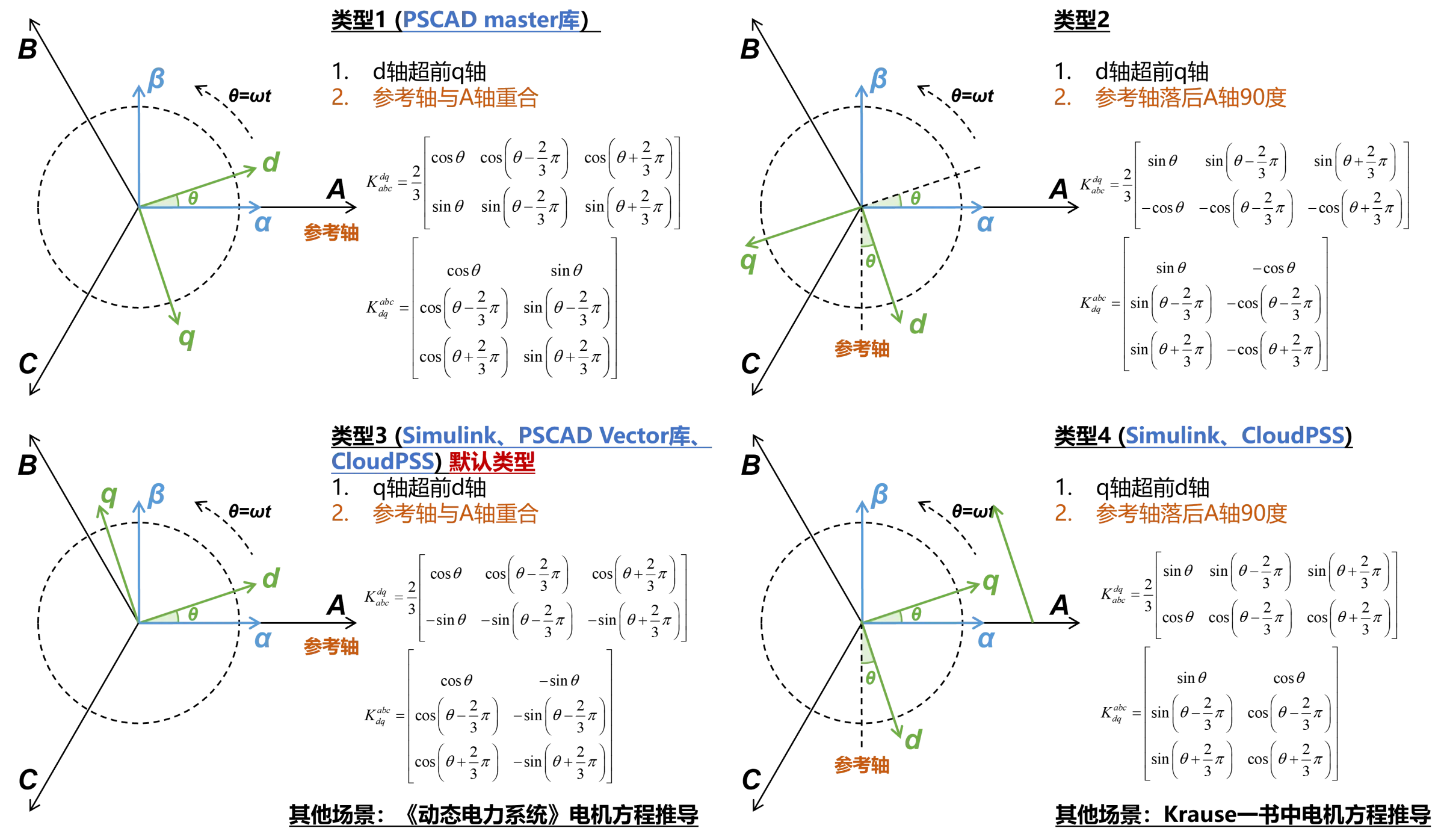四种Park变换类型
四种Park变换类型

案例​

常见问题​