基于 SDK 的 VPP 运行优化
功能介绍
使用 IESLab SDK 实现获取获取算例拓扑、负荷、电价、设备模型等基础参数,借助 Pyomo 等建模工具建立优化模型,编写目标函数、约束条件等,利用 gurobi, cplex,scip, ipopt 等求解器优化计算, 并分析结果。
背景
在新电力系统转型建设的背景下,大量分布式能源涌入配电系统,充电汽车等可调负荷不断接入配电系统,使得电网越来越灵活,且近年来极端天气频发使得预测和控制各类负荷变得越来越困难,电力系统的电力平衡困难、供电可靠性和电能质量下降等问题越来越迫切,需要提高系统的灵活性和可靠性,控制可调资源。
在此背景下,具有灵活资源协调和控制的虚拟电厂(VPP ,Virtual power plant)已成为新型电力系统提高灵活性和电能质量的关键技术和研究方向。虚拟电厂通过通信技术和软件实现了需求响应和协调控制,汇集了许多分散的柔性负载、储能系统和分布式资源,具有大容量统一灵活的调节能力。
VPP 可简单分为技术 VPP 和商业 VPP ,技术 VPP 主要侧重于供电质量和满足电网调度要求,参与辅助服务市场(ASM),以确保配电网的稳定运行;商业 VPP 主要关注交易系统中的能源和其他电力市场。目前,国内的 VPP 主要是基于技术的,对 VPP 的商业价值关注较少。主要功能是需求响应,主要利用分时电价等价格因素,在极端条件下及时实现有序用电,保证供电可靠性和电网稳定运行。
项目介绍
项目位于江南某光伏示范地区,项目地的配电网主要有两个 110kV 变电站。1 号变电站有 1 个分布式光伏电站、风力发电机和用户负荷,主要是光伏溢出区。变电站 2 有 2 个光伏电站和一些用户负荷。三个光伏场站都存在严重的源荷不平衡现象。
配电系统的拓扑结构如所示:
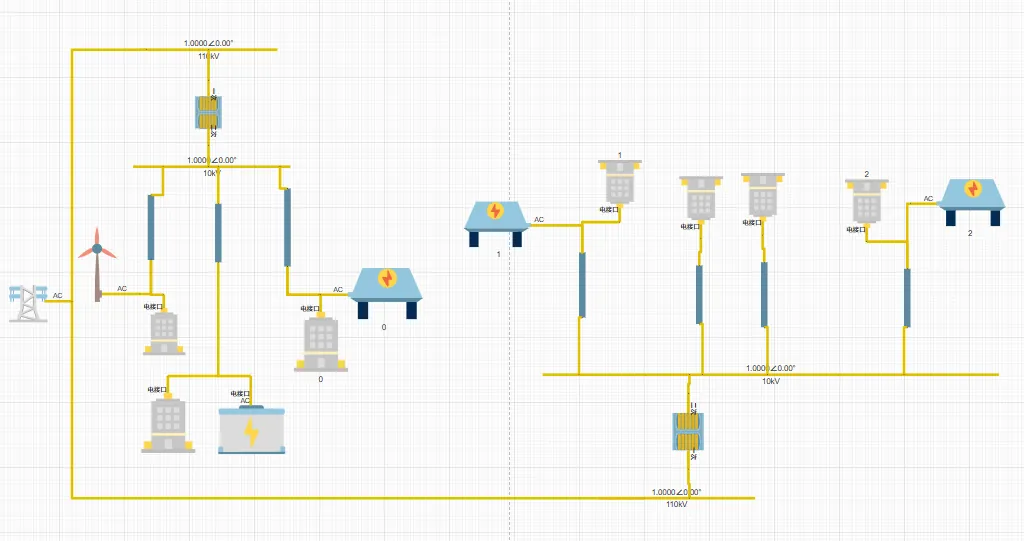
该地配电网光伏消纳能力有限,发送电功率有限,线路最大负荷容量 7.5 M,主要存在电能质量低,负载率高等供电可靠性隐患。
光伏场站 VPP0 最大反向功率 0.55 MW(反向负荷比 7.3%),光伏场站 VPP1 最大反向功率 1.16 MW(反向负荷率 15%),光伏场站 VPP2 无反向功率,光伏线路反向功率导致电能质量下降;
光伏场站 VPP0 的负荷为 2.03 MW(负荷比率 27.07%),光伏场站 VPP1的最高负荷为 5.40MW(负荷率 72%),光伏场站 VPP2 的最高负荷为 3.62 MW(负荷比 48.27%),部分线路的高负荷率对供电可靠性构成隐患。
拟连通三个光伏场站,通过建设 VPP 进行灵活调配,解决该地的源荷不平衡问题。
结果分析
优化结果表明:
- P2P VPP 交易有助于将峰值负载从 VPP1 转移到负担较轻的 VPP2,有效地缓解了电力消耗的急剧飙升。这确保了每条线路的负载系数不超过 60%,减轻了峰值转移期间外部电网的压力,减轻了配电网负载压力,并抑制了电压波动。
- 经济分析显示,通过 VPP 优化,该配电系统的电费从 85482 元/天减少到 81400元/天,每天节省 4081 元,VPP 明显提升了经济效益。
- 此外,通过 VPP 能源交易提高了系统供电可靠性。由于两条线路的总输电容量为 15MW,三个负载的峰值电力需求仅达到 10.5MW,该系统即使在重负荷期或故障期间也能保持稳定运行和供电可靠性。
- 借助 IESLab 平台和 SDK,不仅可以实现规划优化,还可以进行仿真验证;不仅可以使用 IESLab 平台提供的丰富设备模型,还可以自定义设备模型。 IESLab 平台和 SDK,可以帮助用户实现无限可能。
常见问题
- 为什么不直接写优化程序,而是需要借助 IESLab 平台和 SDK?
-
IESLab 平台提供了可视化的拓扑展示界面,提供了丰富的设备模型及参数,能够分类录入管理基础项目数据, SDK 可以便捷获取平台参数,且规划后的结果可以通过 SDK 返回到IESLab 平台进行仿真计算,来验证规划优化结果,这是独立编程规划优化并仿真验证很难做到的; 此外,IESLab 平台提供了原生的稳态设备模型,用户可以直接调用计算结果,无需编写设备模型;同理,IESLab 平台提供的稳态设备模型无法满足需求,也可以自定义设备模型进行编程实现,如在本示例代码中,没有使用平台光伏计算结果,而是自行编写了计算光伏出力曲线的算法。
示例代码
import os
import sys
import time
import cloudpss
import math
import numpy as np
import pyomo.environ as pyo
sys.path.append(solver_path) # Gurobi,Cplex,SCIP,GLPK,COPT
def calc_pv_output(dict_comp,curve_atmos):#计算光伏出力曲线
curve_photovoltaic=[]
for pv in dict_comp['photovoltaic']:
curve_photovoltaic.append([])
for i in range(24):
MINIVALUE=10**(-6)
dirSunshineIntensity = float(curve_atmos[i]['adj_sfc_sw_direct_all_1h'])
diffSunshineIntensity = float(curve_atmos[i]['adj_sfc_sw_diff_all_1h'])
airTemp = float(curve_atmos[i]['t10m']) -273.15
zennithAngle = float(curve_atmos[i]['solar_zen_angle_1h'])
conversionEfficiency=1
for LossCoe_info in pv['args']['LossCoes']:
LossCoe = float(LossCoe_info['1'])*0.01
conversionEfficiency *= LossCoe
dipAnlge = float(pv['args']['DipAngle']) if float(pv['args']['TrackingMethod'])==0 else zennithAngle
hAngle = 90 - zennithAngle
panelDirSunIntense = (dirSunshineIntensity / (math.sin(hAngle * math.pi / 180.0) + MINIVALUE)) * math.sin((hAngle + dipAnlge) * math.pi / 180.0) + diffSunshineIntensity
cellTemperature = airTemp + 0.03 * panelDirSunIntense
deltaI = panelDirSunIntense / 1000.0 * (1.0 + float(pv['model']['ratedParam']['TemperatureCoefficientsofIsc'])*0.01* (cellTemperature - 25.0))
deltaU = (1.0 + float(pv['model']['ratedParam']['TemperatureCoefficientsofVoc'])*0.01 * (cellTemperature - 25.0)) * math.log((math.exp(1.0) + 0.000288 * (panelDirSunIntense - 1000.0)))
power = float(pv['model']['ratedParam']['MaximumPowerVoltage'] )* deltaU * float(pv['model']['ratedParam']['MaximumPowerCurrent']) * deltaI *conversionEfficiency / 1000.0
curve_photovoltaic[-1].append(power)
return curve_photovoltaic
if __name__ == '__main__':
#设置网站环境
os.environ['CLOUDPSS_API_URL'] = 'https://cloudpss.net/'
#申请并设置自己账户的token
cloudpss.setToken(token)
# 规获取指定 simuid 的项目
plan_project = cloudpss.IESLabPlan.fetch(simuid)
#获取算例的基础数据
plan_data_manage = plan_project.dataManageModel
#获取算例拓扑文件
plan_model = plan_project.model
plan_topology = plan_model.fetchTopology().components
# 遍历拓扑文件,根据绑定的设备id,后续可从数据管理模块获取设备参数
map_comp = {'photovoltaic':'DeviceSelection','battery':'DeviceSelection','power_source':'DeviceSelection','electric_load':'ElectricalLoad'}
dict_comp = {comp: [] for comp in map_comp.keys()}
for key_topo, value_topo in plan_topology.items():
for key,value in map_comp.items():
if key in key_topo:
dict_comp[key].append({'args':{},'model':{}})
dict_comp[key][-1]['args'] = value_topo.get('args')
model = value_topo['args'].get(value)
if model:
dict_comp[key][-1]['model'] = plan_data_manage.GetDataItem(model)
break
dict_curve = {}
# 获取购电价格与负荷的售电价格
map_curve = {'PurchasePriceModel':'power_source','PowerPriceModel':'electric_load'}#分时电价
for key, value in map_curve.items():
dict_curve.update({key: [float(plan_data_manage.GetDataItem(dict_comp.get(value)[0]['args'][key])
['purchasePriceModel']['params'][0]['value'][i][0]) for i in range(24)]})
# 获取电负荷曲线
load_param = plan_data_manage.GetDataItem(dict_comp['electric_load'][0]['args']['ElectricalLoad'])['loadParam']
if load_param['model'] == 'rough':
dict_curve.update({'electric_load':[float(load_param['rough_load']['loadcurvedata'][0][0][i]) for i in range(24)] })
elif load_param['model'] == 'custom':
dict_curve.update({'electric_load':[float(load_param['custom_load']['data'][i][1]) for i in range(24)] })
elif load_param['model'] == 'detail':
dict_curve.update({'electric_load':[float(load_param['detail_load']['workAndOFF_Load'][8]['work'][i]) for i in range(24)] })
# 获取气象数据及光伏出力计算曲线
curve_atmos=plan_data_manage.GetAtmosData('2021-09-01', '2021-09-01')
#取一个光伏元件的出力曲线
dict_curve.update({'photovoltaic':[power*1000 for power in calc_pv_output(dict_comp,curve_atmos)[0]]})
# Pyomo 优化建模
model = pyo.ConcreteModel()
# 声明index集合
model.N24Set = pyo.Set(initialize=range(24)) #24 hour optimization
model.N1Set = pyo.RangeSet(0, 0, 1) # 仅需一个索引引脚即可
# 参数,主要是电池和电价
param = {}
param['max_power_supply'] = (float(dict_comp['power_source'][0]['args']['MaxiumPowerSupply']))
param['charge_efficiency'] = (float(dict_comp['battery'][0]['model']['ratedParam']['ChargingEfficiency'])) # charge effiency
param['charge_max'] = (float(dict_comp['battery'][0]['model']['operationalConstraints']['MaxChargingPower']))
param['cap_batt'] = ( float(dict_comp['battery'][0]['model']['operationalConstraints']['PowerStorageLimit']))
param['cost_batt_purchase'] = ( float(dict_comp['battery'][0]['model']['economicParam']['PurchaseCost'])*10000)
param['cost_batt_fix'] = ( float(dict_comp['battery'][0]['model']['economicParam']['FixedOMCost']))
param['cost_batt_var'] = ( float(dict_comp['battery'][0]['model']['economicParam']['VariableOMCost']))
param['cap_batt_max'] = ( min (5000,float(dict_comp['battery'][0]['args']['MaxStorageCapacity'])))
param['soc_ini'] = (float(dict_comp['battery'][0]['args']['InitialPowerStorage']))
param['soc_max'] = (float(dict_comp['battery'][0]['args']['maxlPowerStorage']))
param['soc_min'] = (float(dict_comp['battery'][0]['args']['miniPowerStorage']))
param['pv'] = (dict_curve['photovoltaic'])
param['purchas_price'] = (dict_curve['PurchasePriceModel'])
param['sale_price'] = (dict_curve['PowerPriceModel'])
param['load_elec'] = (dict_curve['electric_load'])
# 定义变量
# 考虑储能台数配置
model.num_batt = pyo.Var(model.N1Set, within=pyo.NonNegativeIntegers,initialize = int(param['cap_batt_max'] / param['cap_batt']),
bounds=(0, int(param['cap_batt_max'] / param['cap_batt'])))
model.charge = pyo.Var(model.N24Set, domain=pyo.Reals,initialize = 0)
# 考虑储能的SOC(荷电状态),定义一个SOC变量
model.soc = pyo.Var(model.N24Set, domain=pyo.NonNegativeReals,initialize = param['soc_ini'] * param['cap_batt_max'])
model.power_supply = pyo.Var(model.N24Set, domain=pyo.Reals,initialize =[a - b for a, b in zip(param['load_elec'], param['pv'])], bounds=(-param['max_power_supply'], param['max_power_supply']))
# SOC(荷电状态)和外部供电量的松弛变量
model.soc_end_slack = pyo.Var(model.N1Set, domain=pyo.Reals, bounds=(-0.1,0.1),initialize =0)
# 定义目标函数,最小化成本
def cost_rule(model,t): # 购电费-售电+最大供电量越限惩罚+充放电运维成本+电池投资 + SOC始末不等惩罚
return sum(param['purchas_price'][t] * model.power_supply[t] - param['sale_price'][t] * param['load_elec'][t]
# + 100 * model.power_supply_slack[t]
+ abs(model.charge[t]* param['cost_batt_var'])
for t in model.N24Set) + param['cost_batt_purchase'] * model.num_batt[0] / 10 / 365 + model.soc_end_slack[0] * param['cap_batt'] * 100
model.obj = pyo.Objective(rule=cost_rule, sense=pyo.minimize)
# 定义约束
# 充放电功率,负荷,外部电源之间的关系
def c1_energy_balance(model, t):
return param['load_elec'][t] + model.charge[t] - param['pv'][t] - model.power_supply[t] == 0
model.c1 = pyo.Constraint(model.N24Set, rule = c1_energy_balance)
#SOC的计算
def c2_soc(model, t):
if t == 0:
return model.soc[0] == param['soc_ini'] * model.num_batt[0] * param['cap_batt']
else:
return model.soc[t] == model.soc[t-1] + model.charge[t]* param['charge_efficiency']
model.c2 = pyo.Constraint(model.N24Set, rule = c2_soc)
# SOC始末相等的松弛
def soc_end(model):
return model.soc[model.N24Set.last()] == (param['soc_ini'] + model.soc_end_slack[0]) * param['cap_batt']
model.c3 = pyo.Constraint(rule = soc_end)
# 充放电功率上下限
def charge_limit(model, t):
return model.charge[t] <= param['charge_max'] * model.num_batt[0] *param['cap_batt']
model.c5 = pyo.Constraint(model.N24Set, rule = charge_limit)
def charge_limit_min(model, t):
return -param['charge_max'] * model.num_batt[0] *param['cap_batt'] <= model.charge[t]
model.c4 = pyo.Constraint(model.N24Set, rule = charge_limit_min)
def discharge_limit(model, t):
return model.discharge[t] <= param['charge_max'] * model.num_batt[0] *param['cap_batt']
model.c6 = pyo.Constraint(model.N24Set, rule = discharge_limit)
#SOC上下限
def soc_min_limit(model, t):
return param['soc_min'] * model.num_batt[0] * param['cap_batt'] <= model.soc[t]
model.c7 = pyo.Constraint(model.N24Set, rule = soc_min_limit)
def soc_max_limit(model, t):
return model.soc[t] <= param['soc_max'] * model.num_batt[0] * param['cap_batt']
model.c8 = pyo.Constraint(model.N24Set, rule = soc_max_limit)
# 储能不能同时充放电的约束
def charge_binary(model,t):
return model.charge[t] * model.discharge[t] == 0
model.c4 = pyo.Constraint(model.N24Set, rule = charge_binary)
# 指定并调用求解器求解:gurobi,cplex,scip,ipopt
solvername='scip'
pyo.SolverFactory(solvername,solver_io="python").solve(model).write()
# model.pprint()
result = {}
result['charge'] = [model.charge[i]() for i in model.N24Set]
result['power_supply'] = [model.power_supply[i]() for i in model.N24Set]
result['soc'] = [model.soc[i]() for i in model.N24Set]
# 结果分析处理
obj_values = model.obj() # 提取最优目标函数值
print("optimal objective: {}".format(model.obj()))
# 也可以后续再读取结果文件,并分析结果
time_result = time.time()
filename= 'id{}_34_result_{}.txt'.format(simuid,time.strftime('%Y-%m-%d-%H-%M-%S'))
with open(filename, 'w', encoding='utf-8') as f:
model.pprint(f)